THE ABRAMS’ STORMTROOPER AXIOM

by David Ng

It (hypothetically*) goes like this:

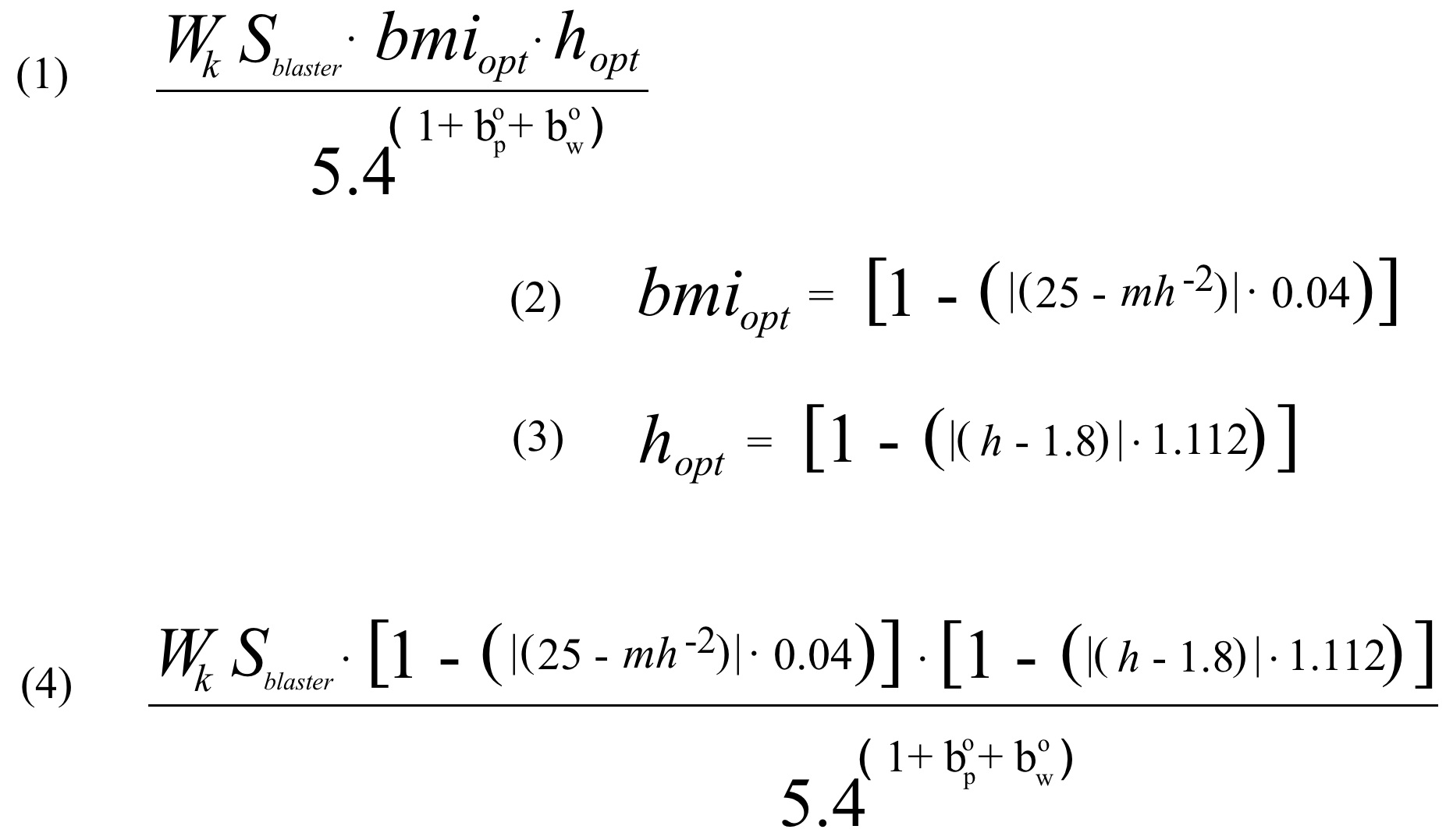
* Like all good science, this needs some testing…

– – –

When news hit that Disney bought the rights to Star Wars, and that J.J. Abrams would be manning the first movie of a new trilogy, my inner geek went into giddy overdrive. This was because it gave me a chance to revisited my bucket list, which had previously scratched off “be an extra in a Star Wars movie” as something that was unattainable having presumed the prequels were my last chance. But now, there is (literally), A NEW HOPE. Even better, is the fact that my kids are old enough to also want this.

And so, being a science-y sort and all, I figured the first step would be to actually try and come up with a way to calculate the odds of such a thing happening, and hence you see the above – or what I have termed the Abrams’ Stormtrooper Axiom. In effect, this is an equation that aims to calculates the odds of you (or anyone) being cast as a stormtrooper in one of these new movies¹.

Here’s how it works. We’ll first look at (1) which expresses the equation in its most obvious form.

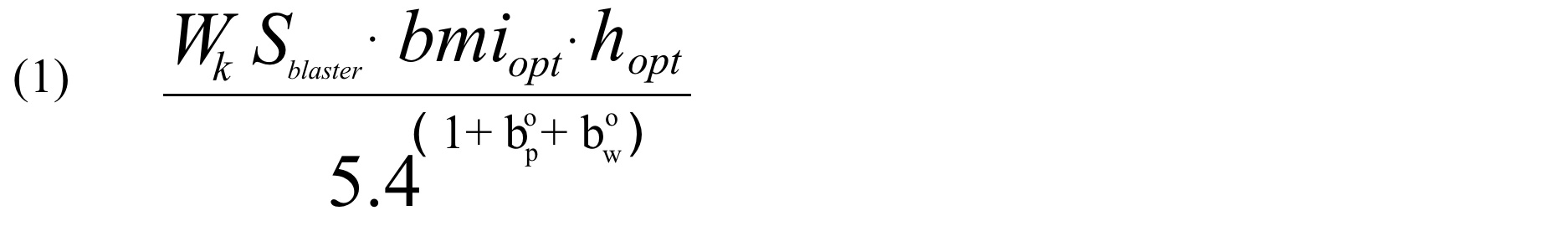
When you look at this equation, there are three main components: two in the numerator: W_kS_blaster and bmi_opth_opt

And one in the denominator: 5.4^(1+b^o_p+b^o_w).

The denominator is an expression designed to address the likelihood of being cast, as having a dependence on the individual’s chance of contact with J.J. Abrams. Specifically, b^o_p refers to the degrees of personal separation the individual is from the Director, whereas b^o_w refers to the degrees of internet separation the individual is from the Director. The base of the exponential relationship is, of course, the standard May The Force Be With You Constant (or 5.4).

All told, if you have very little connection to the director, your odds can dwindle significantly, about 5.4^(1+6+6) times, or roughly one in 3.3 billion! It also infers that even if you know JJ Abrams personally, it does not guarantee being cast – mathematically, the closest association would still work out to 5.4^(1+1+1), or roughly a chance of one in 158. This is because there are other factors that need to come into play when determining whether an individual is right for a stormtrooper part.

Which is where the numerator expressions exert their influence. We can first begin with the bmi_opth_opt element, which essentially considers the physicality of the individual vying for a stormtrooper part. The bmi portion considers body shape, whereas the h portion considers height.

Each element can be further derived as:

Where (2) calculates divergence from an average body type (as expressed by an individual’s body mass index with m equals to the individual’s weight in kilograms, and h is equal to the individual’s height in metres). You’ll note that the more you veer away from an “average” body type, the greater the modification of the bmi_opt number to a number less than one (and therefore further lowering your odds).

In the same manner, (3) calculates divergence from an optimal height (deemed 1.8 metres as determined from casual examination of Star Wars’ trivia – i.e. calculating Mark Hamill‘s height and noting the “Aren’t you a little short to be a Stormtrooper?” comment). Like the BMI calculation, the more you deviate from the optimal height, the greater the modification of the h_opt number to a number less than one (and therefore further lowering your odds).

Note that both (2) and (3) are included in the overall equation for pragmatic prop design reasons (not every extra can have a custom made set of armour, so it makes sense if casting aimed for similar body types). Then, of course, there is the whole clone army narrative which might also presume the troops having similar physical features. (Also note that in case you weren’t familiar with the symbol, the straight up and down lines enclose a value where you only use the absolute number – i.e. remove the plus or minus sign).

Anyway, when you put it all together you get the expression (4).

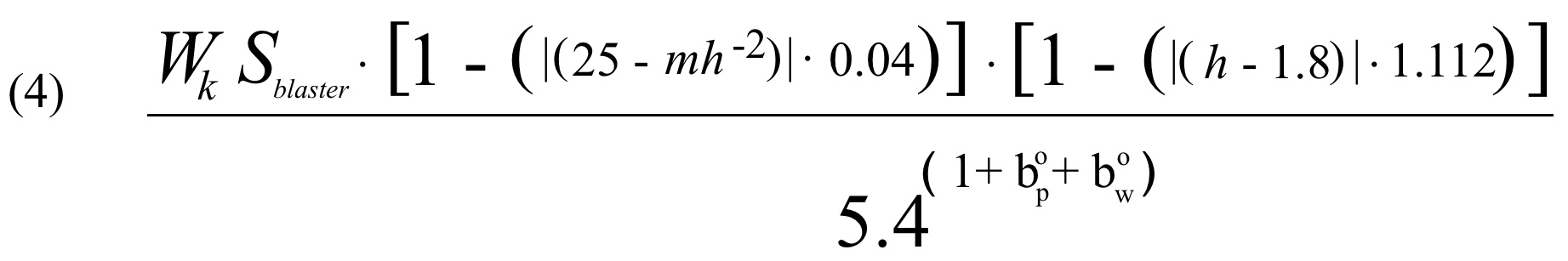
Which only leaves W_k and S_blaster to be defined. Here, these two variables relate to two specific personality traits that are deemed important for the stormtrooper casting decision.

For instance, I don’t think I’m the only Star Wars fan who notices the incredibly poor marksmanship exhibited by the stormtroopers. There are many instances in the movies where there are many of them (with their weapons – presumably high tech in nature), in close proximity to the target, and yet, they still always fail to hit their target.

Given this observation, I’m left to assume that Stormtroopers, as a whole, have a deep distrust of guns, and with that discomfort tend to misfire (perhaps subconsciously). This also leads me to hypothesize that not only are they not very skilled, but that they are probably the sort that are not at all familiar with gun culture in their private lives.

Consequently, S_blaster is a number assigned to measure the individual’s relative experience wth guns, whereby a value of 1.0 represents full disconnect from the use of guns in their personal lives, and a number closer to zero represents an individual who is very familiar with gun culture.

Of course, perhaps the most important tangible characteristic (that could translate to a positive casting decision) is relative fandom itself. In other words, casting may be partly governed by how “into Star Wars” an individual is. Here, and in honor of Chewbacca’s reference of “pulling arms out of their sockets when they lose,” I’ve decided to use Wookie knowledge, or W_k as an indicator that can further increase casting chances. Essentially, this is a scale that ranges from 1 to 10, whereby 10 represents fanatical knowledge on all things Wookie, and 1 represents no knowledge at all. In effect, if you’re nuts about Star Wars (and wookies specifically), you can increase your chances of being cast by 10 fold.

In conclusion, I want to stress that this is the Abrams’ Stormtrooper Axiom, and by its very definition, an axiom is just a starting point. This means the equation will need more work, and it would be great suggestions to make it better. As it stands, it works as a general guideline using a number of test values². As well, there is also the very real caveat of whether J.J. Abrams will even have stormtroopers in the new movies – never mind the fact that if he does, they may come in a different size, or be better at shooting, etc. In some respects, this reminds me a little of Schrödinger’s cat (we can call our version Abrams’ Stormtrooper): we won’t really know what he has in mind until he lets us open the box.

– – –

Footnotes

1. In general, I’ve used information from the original trilogy for points of reference.

2. For instance, an individual with no connection at all will result in a number that works against the backdrop of the total human population numbers. For J.J. Abrams, himself, where b^o_p and b^o_w are equal to zero, and his W_k is likely quite high, the equation would further calculate that he has practically perfect odds of being cast as a stormtrooper (which makes sense given his role in the movie). For the sake of comparison, I’ve calculated my own odds to be approximately: 0.00000519 or about one in 19,000.