How To Fly
“The knack of flying is learning how to throw yourself at the ground and miss”
With these words, Douglas Adams helpfully explained concept of flying in his Hitchhiker’s Guide to the Galaxy. But the ground is really big, and, as the Tick so sagely noted, “Gravity is a harsh mistress.” So herein contained is my handy-dandy explanation of how you can impress your friends and family by throwing yourself at the ground and missing:
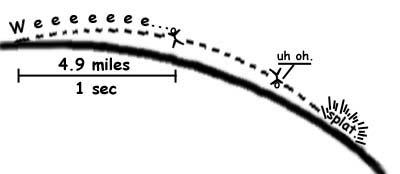
Step one, throw yourself at the ground. Luckily, this is really easy thanks to gravity, which will pull you down to the ground at an acceleration rate of 32.174 feet per second per second, meaning every second you are falling to the ground, you fall 32 feet (9.8 meters) per second faster. If you want to fall for one second, just spend enough energy to climb 16 feet (4.9 meters) above ground and drop. Voila!
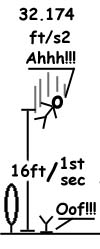
Step two, miss. This is the not so easy part. If you’re reading this, then I assume you are a nerd (like me) and probably still wake up some nights in a cold sweat with nightmares about dehumanizing games such as “Dodge Ball” and possibly even it’s more sadistic cousin “Smear the Queer” from your youth. Now we’re trying to dodge a planet 7926.28 miles (12756.1 kilometers) across at the Equator. Might as well just throw in the towel and brace ourselves for the wedgies, noogies, and nipple cripples. Right?
WRONG!
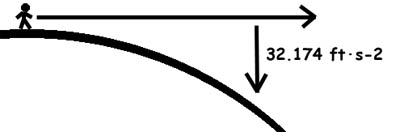
We don’t have to miss the whole Earth at once, just enough to keep from hitting it each moment. The Moon does this all the time, dodging the Earth faster than it falls toward it – and it’s just a big dumb rock. We don’t want to be dumber than a rock, do we?
Okay then. All we have to do is dodge faster than we fall.
If we fall 16 feet (4.9 meters) in the first second, then we simply have to dodge far enough for the Earth to curve away 16.087 feet below us in one second. Knowing how far to dodge is, as G.I. Joe so wisely said, “half the battle.”
Which brings me to step three, find someone who knows math. In my case, I contacted my brother, Para, who teaches Multivariable Calculus at Georgetown Day School in Washington DC.
Para drew an angle on my circle representing the Earth, “It’s real simple,” he said. “See, sine is the opposite divided by the hypotenuse, cosine is the adjacent divided by the hypotenuse, and tangent is opposite divided by the adjacent. SOHCAHTOA, or Some Old Horse Caught Another Horse Taking Oats Away.” He drew a bunch of equations out for me. “See?”
“Huh,” I muttered.
“I’ve lost you, haven’t I?”
“Um,” I thought about lying, but he’s my brother, he can tell, “yeah.”
“Didn’t you take Trigonometry in high school?”
“Triggawhatromee?”
“Okay,” Para put the pen to his mouth thoughtfully. “I think I see a way to do this with just algebra.”
“Algebra… That sounds familiar. That’s math, right?”
“Hush,” Para drew the following diagram:
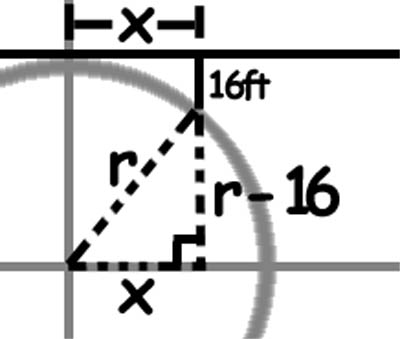
Where x is the distance we have to travel for the Earth to curve 16 feet away from under our feet and r is the radius of the Earth. Because we have right triangle and know the radius of the Earth is 20,925,379.2 feet (6.378,055.6 meters), we can use the Pythagorean theorem to find x, like so:
Which, Para showed me, can be converted to:
And then, according to Para, the r’s cancel out, leaving us with:
Which means x equals the square root of 32r + 256! (Once again, according to Para, so if this is wrong, blame him.)
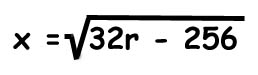
Plug 20,925,379.2 feet (6.378,055.6 meters) into r and we find that we have to travel 25,876.9 feet (7,887.2 meters) or 4.9 miles (7.0 kilometers) in one second to successfully keep from hitting the Earth. Case closed right?
WRONG! SIT BACK DOWN!
We’re still accelerating towards the Earth. So we’re traveling at 32 feet per second after one second, 64 ft/s after two seconds, 96 ft/s after three, meaning we have to travel far enough for the Earth to curve away from under us by 80 feet in three seconds! And we’re only going to fall even faster after that.
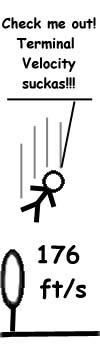
Luckily, the Earth’s atmosphere produces a drag on us as we fly. So we can only fall so fast toward the Earth. The speed at which we can’t fall any faster because the air is slowing us down is called Terminal Velocity, and it means that the fastest a person can fall to Earth is 120 MPH (193.1 km), or 176 feet (53.6 meters) per second–if we keep our arms spread out to increase drag.
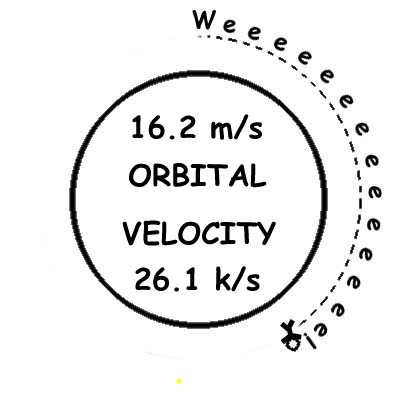
So that translates to us having to dodge the Earth at 85,823.7 feet per second to achieve orbital velocity. That’s 16.2 miles (26.1 kilometers) per second in order to fly. So let’s all go fling ourselves off the Earth right away! Right?
WRONG!
If everybody else jumped off a bridge would you? Shame on you! There’s still a few safety considerations we need to factor in to this.
For instance, meteors burn up in the atmosphere because they are traveling 26 miles (41.8 kilometers) per second. We’ll be traveling about 62.3 percent of that velocity. Not enough to FOOM! burn up in the atmosphere, but we should probably pack some SPF one-bazillion sun tan lotion for the trip just in case.
There’s also the speed of sound, which is 761.2 mph (1,225 kph) at sea level. So we’ll be traveling 76.6 times faster than the speed of sound, so we should probably pack earplugs and leave the ipod at home.
The speed of light is 186,282.4 miles (299,792.5 kilometers) per second, and we’ll be traveling at 0.0009 percent of this speed. So we don’t need to be worried about hurting the feelings of all the physicists in the world by breaking the laws of their discipline.
The last thing we need to consider is that it’s going to take at least 25 minutes and 36 seconds to fly all the way around the Earth and back to where we started. So we better make sure to let our moms know when we’ll be getting back so they don’t worry. Okay?
Now can we fly now? Huh? Can we? Can we? Can we?
YES!!!
Congratulations! You now know how to throw yourself at the ground and miss, effectively flying!
Since I can’t copyright this knowledge, please remember, when you accept your X-Prize one day, be sure to mention me in your acceptance speech.