JEEZ, THESE THINGS COULD COMPUTE! (A PRIMER ON DNA COMPUTERS)
In 1947, three physicists and electrical engineers named William Shockley, John Bardeen and Walter Brattain, employed at Bell Laboratories in New Jersey, crudely fashioned a clunky device using paper clips and razor blades, which could control the flow of electric current between two pieces of gold by adjusting the current in a third piece of germanium. This invention, which is now known as a transistor, constituted the world’s first purely electronic switch and is now considered the basic building block for the construction of all machines that process data using electricity.
For their pioneering work, Shockley (whose name, by the way, I have always found humorously appropriate to his field of study) and his colleagues were awarded the Nobel Prize in Physics in 1956. The creation of the transistor immediately set off an explosion of research and investment and spawned new fields of study to both develop new transistor-based machines and engineer smaller and faster switching transistors. This explosion has ultimately resulted in perhaps the most ubiquitous and remarkable piece of modern technology: the computer.
Sixty years after the invention of the transistor, the silicon-based microchips that form the core of today’s computers now contain almost a billion interconnected transistors, which together perform millions of calculations per second. The relentless progression and fine-tuning of manufacturing technology has resulted in factories capable of pumping out transistors so small that hundreds of them could fit onto the surface of a single human red blood cell, and so cheaply that the production cost of a single transistor is now comparable to that of a grain of rice.
Because of the massive intellectual and financial push for progress in the fields of solid-state physics, integrated circuit design, and computer engineering, we now exclusively associate the concept of a “computer” with visions of magical streams of ones and zeroes zipping through metal wires, processed by silicon microchips, and stored in whirring magnetic hard drives. While progress in this direction has been undoubtedly swift and impressive, one might reasonably ask: is this the only way to make a computer? This question naturally begs another: what exactly is a computer? This question was pondered by mathematicians and logicians long before any notion of the modern computer existed.
In 1936, Alan Turing, an English mathematician who is widely regarded as the father of modern computer science, introduced the concept of an abstract but very basic machine known as a Turing machine. Turing did not intend for this machine to actually be built, but brought forth the concept as part of a thought experiment to determine what theoretical limits exist on the calculations possible for any manmade machine. A Turing machine has only two basic requirements: it must be able to store information, and it need only be able to perform a finite number of operations using that information as the input. Turing’s example of such a machine is an imaginary contraption that has as its input a length of tape inscribed with a series of symbols from a finite alphabet. The imaginary contraption is granted only the ability to read a symbol and, based on what that symbol is, write a symbol from the same finite alphabet and then move left or right by one symbol along the tape – an incredibly simple machine. What Turing famously concluded and proved in the so called Church-Turing thesis is that any mathematically definable calculation can be carried out by this machine given a long enough length of tape and enough time. In other words, anything that can be computed can be computed with Turing’s imaginary tape-processing machine.
In reality, of course, a calculation of any considerable complexity would require an impractical amount of both tape and time. Turing’s conclusion, however, is nonetheless a powerful one. If we now take the Turing machine to be our definition of a computer, it becomes immediately clear that a great many things can be used to compute. Surely the transistor-based electricity-manipulating boxes that so many of us have on our desks can not be the only things that satisfy Turing’s definition of a computer.
Around the same time that Shockley and his colleagues were occupying themselves with the business of refining the design of the transistor (and embroiling themselves in heated arguments over patent rights), James Watson and Francis Crick were at work attempting to develop a structural model for nature’s information-carrying molecule, DNA. Their work revealed the now classic double-helix structure of DNA and the existence of Watson-Crick pairs of nucleotides which allowed for the explanation of the process by which DNA is replicated. Their work pioneered the now rapidly growing field of molecular biology and earned them the Nobel Prize in Medicine in 1962.
As it is now well-known, the DNA molecule replicates by first being separated into two strands by the protein helicase. Each of these strands is then operated upon by another protein called DNA polymerase which reads each nucleotide in the strand and then connects it to its Watson-Crick complementary nucleotide, thus forming two new double-stranded molecules. As this process is required for cell division in every known life form, it is the key to the reproduction of all living things and is performed using extremely effective error-checking and proofreading mechanisms to ensure that identical copies are produced. When Watson and Crick discovered this process of DNA replication, it is unlikely that they were thinking of it in anything other than a purely biological context. After all, even now, when one first learns of the central dogma of molecular biology which stemmed from their discovery, it is hard to think about much other than the profound implications it has on life itself.
However, one night in 1993 while lying in bed next to his wife reading the classic textbook co-authored by James Watson, The Molecular Biology of the Gene, a mathematician and computer scientist named Leonard Adleman noticed a very interesting similarity while reading about DNA polymerase. He realized that it is in essence a Turing machine. This realization prompted him to sit up and exclaim to his wife, “Jeez, these things can compute!”
Indeed, considering the similarity between the process by which DNA polymerase travels nucleotide by nucleotide along a single strand of DNA adding Watson-Crick complements, and Alan Turing’s machine that travels symbol by symbol along a piece of tape writing pre-programmed symbols, it is somewhat surprising that this connection was not made earlier. Adleman stayed up the rest of that night figuring out how to put billions of years of evolution to work on mathematical problems. Turing’s work had shown that performing computation using DNA was possible and Watson and Crick’s work gave a description of the available tools. Adleman just had to figure out how to combine them.
The problem that Adleman decided to solve using no keyboards, transistors, or anything else reminiscent of a modern-day computer, is commonly known as the traveling salesman problem. Given a number of planets that an alien intergalactic salesman must visit, and given a series of one-way interplanetary space flights connecting the planets, the problem is to determine whether there is a sequence of flights that will allow the salesman to start at a designated “start planet”, visit each planet only once, and end at a designated “end planet” (as you might have guessed, I have taken the liberty of altering certain aspects of the classical presentation of this problem). For example, in the graph below, where arrows represent one-way flights, only one such sequence exists for a start planet of Alderaan and an end planet of Dagobah, and it is Alderaan to Hoth to Bespin to Dagobah.
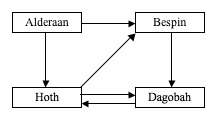
For a small number of planets, as in the example above, the problem is intuitively easy to solve. However, as the number of planets grows, it becomes much more difficult. More formally, this problem is known as the Hamiltonian Path Problem, where the planets are called vertices, the flights are called directed edges, and the sequence in question is called a Hamiltonian path. This problem is significant in the field of computer science because, so far, no algorithm has been discovered which will solve it quickly (for those with a thorough understanding of complexity theory, which I am not one of, the problem is classified as being NP-complete).
For certain graphs with fewer than 100 vertices, it would take the fastest silicon-based computers running the fastest known algorithms hundreds of years to determine whether a Hamiltonian path exists. The graph that Adleman set out to solve using his proof-of-concept DNA computer is this 7-vertex, 14-edge graph:
Adleman decided to implement the following algorithm for finding a Hamiltonian path through n vertices:
I. Generate a set of random paths through the graph.
II. For each path in this set do the following:
A. If the path starts at the designated start vertex and ends at the designated end vertex, keep it. If not, remove it from the set.
B. If the path passes through exactly n vertices, keep it. If not, remove it from the set.
C. If the path passes through every intermediary vertex (all vertices except the start and end ones) in the graph, keep it. If not, remove it from the set.
III. If the set is not empty, then there exists a Hamiltonian path. If it is empty, then there exists no Hamiltonian path
He began by first assigning random DNA sequences to each of the planets in the graph. It is helpful to think of these sequences as having a first and last part. If we consider our simpler 4-planet example, then Alderaan can be assigned a sequence of 1a1b (where 1a is the first part of the sequence and 1b is the last part), Hoth can be assigned a sequence of 2a2b, Bespin can be assigned a sequence of 3a3b, and Dagobah can be assigned a sequence of 4a4b, where these sequences are each L nucleotides long. From Watson and Crick’s work, we know that every DNA sequence has a complement. So the complement of the Alderaan sequence becomes 1a’1b’, where x’ is the complement for sequence x.
Next, he assigned each one-way flight a DNA sequence such that the flight names were composed of the last part of the planet of origin followed by the first part of the destination planet. So, for example, the Alderaan to Hoth flight was assigned a sequence of 1b2a. Adleman then had all of the planet sequences, the planet sequence complements, and the flight sequences manufactured. He then simply placed these sequences into a test tube with ligase (a protein that is capable of binding two DNA molecules end to end to form a single molecule), some salt to adjust the pH, and some other ingredients to form a cocktail designed to simulate the conditions inside a living cell.
The moment these sequences were placed together in the tube, many random molecular binding events were initiated, including several of particular interest. By chance, the Alderaan-to-Hoth flight sequence (1b2a) was bound to the complement of the Hoth sequence (2a’2b’) since 2a will bind to 2a’ due to Watson-crick pairing. By chance again, this sequence was then bound to the Hoth-to-Bespin flight sequence (2b3a) by the same mechanism. In this way, the sequence corresponding to the desired Hamiltonian path began to grow with the flight sequences bound together by the complements of the planet sequences. In our example, it would have looked something like this:
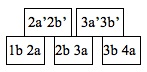
The ligase in the tube would then permanently fuse the flight sequences together end to end. Of course, trillions of other sequences that did not encode a Hamiltonian path were also simultaneously being formed by the same random binding processes in Adleman’s tube. This simple procedure, easily performed in any molecular biology lab, executed a massive number of simultaneous reactions equivalent to an enormous amount of brute-force parallel data processing. This parallelism is the true power of DNA computing. Notice that the random production of these sequences also represents step I of the algorithm above. Adleman’s next task was to isolate the sequence encoding his desired Hamiltonian path from the myriad of other sequences, or in other words, to carry out steps IIA, IIB, and IIC of his algorithm.
To do this, he used some very standard molecular biology techniques. Referring again to our example, Adleman first needed to identify the sequences starting with Alderaan and ending with Dagobah and remove the rest. He did this using polymerase chain reaction (PCR). This procedure exponentially replicates DNA sequences having a specified beginning and end, and was thus perfectly suited for step IIa. By using the last part of Alderaan’s sequence (1b) as the beginning primer and the complement of the first part of Dagobah’s sequence (4a’) as the end primer, a PCR was performed which would selectively amplify sequences starting and ending with the desired planets. The other unwanted sequences would still be present in the tube, but at insignificant quantities compared to the amplified sequences of interest. Step IIA was done.
Step IIB required the removal of any sequences that did not pass through the number of vertices in the graph (4 in this example). This was done by performing a gel electrophoresis which uses an electric field to separate molecules according to their masses. Since the desired sequence is 3L nucleotides long (only 3 flights are required to form a Hamiltonian path between 4 planets), Adleman could isolate his molecules of interest with this method, thereby completing step IIB. The final step of the algorithm required the removal of all sequences that did not pass through the intermediary planets in the graph. To do this, Adleman repeatedly used a procedure known as affinity separation. He first coated balls with sequences complementary to one of the intermediary planets (say Hoth), and placed them in a solution containing the molecules isolated from step IIC. This caused only those sequences containing the Hoth sequence to stick to the balls, while those that did not remained in solution. Adleman could then remove the balls from the solution, strip the desired molecules from their surfaces, place them in another solution, and repeat the separation for all other intermediary planets. This completed step IIC. If, after the last separation, Adleman still had molecules stuck to iron balls, he knew they had to encode the Hamiltonian path. Indeed, he did and the sequence was correct.
The solution to Adleman’s Hamiltonian path problem, which would take most people less than a minute to solve by inspection, required 7 days of lab work to complete. Nevertheless, his experiment, which implemented the first ever DNA computation, definitively proved the computing power of DNA. The parallelism that this kind of computation allows is easy to see. In Adleman’s experiment, approximately 1014 one-way flights were molecularly connected in roughly one second, providing the capability of exploring an incredibly large set of random paths in a very short time.
The information storage density of DNA is another attractive property of this kind of computation. A single gram of dried DNA can store as much information as a trillion CDs. Adleman’s proof of concept generated a wave of interest in DNA computing. Some researchers have tackled the problem of improving the efficiency of the steps required to isolate the solution set, the most tedious part of Adleman’s experiment. Others have explored potentially revolutionary applications of the technology. In 2004, a DNA computer was constructed that could identify and analyze the mRNA of disease-related genes and produce a single-stranded DNA molecule modeled after an anticancer drug in response. One can envision these DNA computers being integrated into human cells to form microscopic medical devices capable of both detecting disease and administering treatment.
Looking back now, we might ask: what if the structure and function of DNA had been discovered earlier? What if Adleman’s revelation had been made before Shockley and his colleagues invented the transistor? Would we all now be running the latest version of Windows on boxes filled with tiny tubes of DNA and proteins? Would the salesman at the local computer store be spouting stats about enzyme kinetics and oligonucleotide lengths instead of processor speeds and RAM sizes? Maybe the answers are yet to come…
Bibliography
Adelman, L. M. Molecular computation of solutions to combinatorial problems. Science 266:1021–1024 (1994).
Adelman, L. M. Computing with DNA. Scientific American, August 1998 p. 34-41 (1998)
Benenson et. al. An autonomous molecular computer for logical control of gene expression. Nature 429: 423-429 (2004)
http://en.wikipedia.org/wiki/Dna_computing, Oct. 9, 2007