THE THEORY OF SPECIAL RELATIVITY… IT’S PRETTY SPECIAL
In 1905 Albert Einstein published a landmark paper concerning the properties of space and time. The theory that he introduced, the so-called theory of special relativity, forced a complete reformulation of our conceptions of these two fundamental structures.
To get a sense of the far-reaching consequences of this theory it is instructive to look at an example. Imagine driving in a car at 100km/h alongside another car (say a Porsche) that is also driving at 100km/h (the velocities of each car of course being in reference to the road). If you looked out the window at the Porsche then it would appear stationary with respect to you, common sense right? Well what happens if instead of a Porsche traveling at 100km/h it is a light beam traveling at the speed of light, and instead of you traveling at 100km/h you’re traveling at the speed of light as well. The same common sense would suggest that the light beam would appear stationary – as the Porsche did in the previous case. It turns out however, that the light beam would in fact be traveling at the speed of light with respect to you as well as at the speed of light with respect to the road. This may seem paradoxical, but through an understanding of the theory of special relativity this paradox can be resolved. This involves however, an understanding of the true nature of space and time. This theory of special relativity is what I will attempt to explain in this paper.
The foundation of special relativity is rooted in two fundamental postulates:
1) The Principle of Relativity and;
2) The Universal Speed of Light
The Principle of Relativity, simply put, states that inertial motion (i.e. constant-velocity motion) is relative. This is best explained through an example.
Imagine waking up in the cabin of a train just as another train passes by on an adjacent set of tracks. If the train ride was perfectly smooth (i.e. did not jostle, shake, change directions or accelerate) then by looking out the window at the adjacent train you may be uncertain whether it was your train, the adjacent train or both trains that were moving. It is not until the adjacent train completely passes by and you are able to reference yourself with respect to land, can you state that your train is moving [1].
This example serves to highlight the notion that there is no state of absolute motion: motion is always with respect to something else (i.e. motion is relative), your moving train is moving with respect to the land.
The Principle of Relativity also implies that there is no physical experiment that can be performed that will allow you to determine your state of motion. Returning to the train example, if when you woke up the shades were drawn and the window was completely covered, then there would be no way for you to determine whether the train was sitting still on the tracks or whether it was in motion (of course you have to assume a perfectly smooth ride again and that you cannot simply pull the shades and look out the window, which is effectively the same as referencing your motion with respect to land).
It is important to note that the Principle of Relativity is specific to constant-velocity motion. If while in the cabin of the train (with the shades drawn covering the window) the train started to accelerate then you would immediately know that the train was moving. This is because you would feel a force pushing you in the opposite direction of the motion of the train (like if in a car that has just accelerated, you’ll immediately get pushed back into your seat).
One last point to mention is that because motion is relative, an observer in motion who is in motion with respect to a ground observer (i.e. a stationary observer) can equally claim that it is he / she who is stationary and that it is the ground observer who is in motion (moving in the opposite direction). This claim is valid because there is no such thing as absolute motion.
To summarize then: The Principle of Relativity states that inertial motion is relative and that there is no way to determine your state of motion without reference or comparison to something else.
Now for the second postulate.
The Universal Speed of Light states that the speed of light (denoted as c, which is roughly 3.00 x 108m/s through air) is the same for all inertial observers (i.e. for all observers in constant velocity motion. This includes observers who are at rest – i.e. not moving – with respect to ground).
This postulate is what gives rise to the paradox mentioned at the beginning. It was a radical idea when first proposed (and you may be thinking that it’s still a radical idea) but all the experimental evidence, related to the properties of light, that was put forth in the late 19th century and beyond indicate that this postulate is in fact true. To illustrate what this means let’s use another example [2] , which will serve to highlight the paradox mentioned at the beginning of this paper.
If I am walking at a speed of 5km/h down the corridor of a train that is moving at 100km/h then my total speed relative to the ground would be 105km/h (100 + 5), or so you think. According to the second postulate, however, if instead of me walking down the corridor it was a beam of light traveling down the corridor then the beam of light would be traveling at the speed of light with respect to the train as well as with respect to the ground (i.e. the speed of light is exactly the same regardless of whether I’m observing the light beam from the train or from the ground). This is why, as per the paradox introduced at the beginning of this paper, the light beam would be traveling at the speed of light with respect to you as well as with respect to the road because it is a requirement of the second postulate of the theory of special relativity. You’re probably unsatisfied with this explanation, and that’s fair because I haven’t given you any reason to be satisfied. But as we’ll see next, it is in the implications of the postulates of special relativity where satisfaction with this answer can be found.
There are three important consequences (with respect to the properties of space and time) that arise due to the two postulates of special relativity. The first is the relativity of simultaneity. This means that two events occurring simultaneously from the perspective of an observer will not (in general) occur simultaneously from the perspective of a different observer who is traveling at a different velocity.
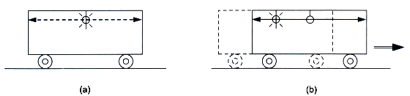
To see this let’s use an example [2]. Imagine a freight car traveling at a constant speed (again assuming perfectly smooth motion) along a straight track (fig. 1.0). In the very center of the car hangs a light bulb. When the light bulb is switched on, the light will spread out in all directions at the speed of light (c). Now an observer in the freight car would conclude that the light reaches the front end of the car at the same instant as it reaches the back end, because the light bulb is equidistant from the two ends (fig. 1.0a). The two events (light reaching the front end and light reaching the back end), occur simultaneously (to the observer in the car). To an observer on the ground however, these same two events are not simultaneous. For as the light exits the bulb, the car itself moves forward, therefore the light heading towards the back end has a shorter distance to travel than the light going forward (fig 1.0b). According to the ground observer therefore, the light reaches the back end of the freight car before it reaches the front end. Hence, the two events are not simultaneous with respect to the ground observer, and that simultaneity of events is dependent on an observer’s state of motion.
If this still seems confusing it may help to recall the last point that I mentioned on the Principle of Relativity. The observer in the car can state with equal validity that it is he / she who is stationary and it is the ground observer who is in motion. From this perspective it is easy to understand why the observer in the car would observe the light reach the front and back end of the car simultaneously, whereas the observer on the ground who observes the car moving (thus the ground observer is stationary now) would state that the light reaches the back end of the car before reaching the front end.
The second consequence is known as time dilation (which is arguably the most intriguing facet of special relativity). It states that time runs slower for observers in motion. Let’s return to the freight car example again to illustrate this point [2].
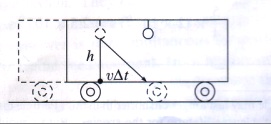
Referring to fig 2: If the observer in the freight car wants to determine the time it takes for the light (upon switching the bulb on) to reach a point on the floor directly below the bulb, the answer would be:

(the overbar on the t denotes measurements made by the observer in the car). With respect to the observer on the ground however, the point on the floor has moved forward upon switching the light bulb on. The time it takes for the light to reach that point on the floor (from the ground observer’s perspective) is:
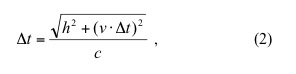
Where v is the velocity of the car. Solving equation (2) for:
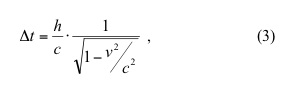
Substituting equation (1) into equation (3), and solving for:
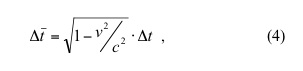
Equation (4) states that the time elapsed between the light exiting the bulb and reaching the point on the floor (directly beneath the light bulb) is different for the two observers, and is in fact shorter for the observer in the freight car. Hence time for the observer on the freight car runs slower compared to the observer on the ground (time dilation).
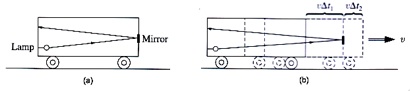
The third consequence is known as Lorentz contraction. It states that moving objects contract in length. As always, this is best illuminated with an example [2].2 Returning to the freight car, imagine that instead of the light bulb hanging from the ceiling it is mounted to the rear end of the car, and that there is a mirror attached to the front end. When the light bulb is switched on therefore, light will travel from the rear-end to the front end of the car and then back to the rear-end (fig. 3.0a).
The question posed is: How long will it take the light to make this round trip? To the observer in the car, the answer is:


To the observer on the ground however, the time it takes to make the round trip is complicated by the motion of the car. Let’s denote the time it takes for the light to reach the front end of the car (from the ground observer’s perspective) by Δt1 and the time it takes to return to the rear-end by Δt2, then (fig. 3.0b):
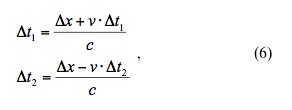
Solving equations (6) for Δt1 and Δt2 gives,
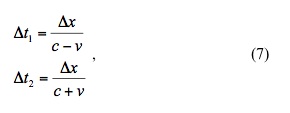
This means that the round trip time (according to the ground observer) is,
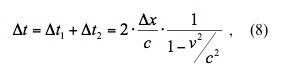
Therefore substituting equation (8) into equation (4) gives,
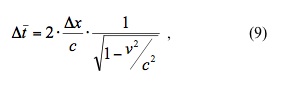
Substituting equation (5) into equation (9) gives,
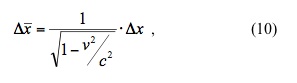
Equation (10) implies that the length of the freight car is not the same when measured by the ground observer, versus when measured by the observer in the car. In fact, from the ground observer’s perspective it has contracted in length (hence the term Lorentz contraction) by a factor of,
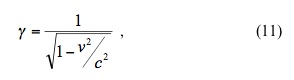
It is important to note that Lorentz contraction is fundamentally different than the type of contraction in length that occurs when you squeeze an object. For when you squeeze an object the decrease in its length is made up by an increase in its height and width. Lorentz contraction, conversely, does not involve changes in the height and width upon contraction in length. It is only the length of the object (as viewed by the ground observer) that will change.
In the above examples we concluded that time for the moving object had slowed down (time dilation) and that the length of the moving object had contracted (Lorentz contraction). This however, is what the ground observer would observe. From the point of view of the observer in motion it is the ground observer whose time has slowed and it is the ground observer (and any objects on the ground) that contracts in length (recall the last point I mentioned in the explanation of the Principle of Relativity).
This raises an interesting paradox: If the ground observer claims that it is the observer in motion whose time has slowed down, and whose length has contracted and the observer in motion is claiming that these effects have not happened to him / her but have happened to the ground observer, than who is right? The answer is that the ground observer is right (although that doesn’t change the fact that the observer in motion would perceive the ground observer as experiencing the effects of special relativity). The reason why the ground observer is correct is because in order for the observer in motion to have entered the state of motion he / she would have accelerated at some point from a state of rest (the same state as the ground observer) to the current state of motion. In which case upon accelerating the observer in motion would be subjected to a force and would feel the effects of entering a new state of motion (recall that the Principle of Relativity only applies to constant-velocity motion). Thus it is the observer in motion who will in fact experience the effects of time dilation and Lorentz contraction despite perceiving otherwise.
The theory of special relativity revolutionized our conceptions of space and time. No longer could we think of space and time as absolute immutable structures, but instead we were required to think of them as dependent on the relative motion between an observer and the observed. It is important to note however, that the effects of special relativity (i.e. the relativity of simultaneity, time dilation and Lorentz contraction) are not apparent until objects are moving at speeds close to the speed of light. This is best understood by examining equations (4) and (10). For speeds like those of everyday objects (e.g. planes, trains and automobiles) the _ factor (equation (11)) is essentially equal to one (the speed of light, remember, is roughly 300,000 km/s) and thus the time and length measured by an object in motion is equivalent to the time and length as measured by an observer on the ground. It is not until an object approaches the speed of light do the effects of special relativity become observable.
References
1. Greene, B. 1999. The Elegant Universe. Vintage Books, New York.
2. Griffiths, D. J. 1999. Introduction to Electrodynamics, 3rd edition. Prentice Hall, New Jersey.