THE SOCIAL NORM OF LEAVING THE TOILET SEAT DOWN: A GAME THEORETIC ANALYSIS
The issue of whether the toilet seat should be left up or down after use seemingly generates a lot of passion among the parties concerned, however, scientific inquiries into the matter are almost non-existent. Notable exceptions are Choi (2002) and Harter (2005). Choi (2002) argues that the rule of leaving the toilet seat down after use is inefficient in the sense that there is at least one other rule that outperform this rule. The unit of analysis in Choi (2002) is the household and the efficient rule is defined as one that minimizes the total cost of toilet seat operations per household. Choi (2002) does not model the issue as a situation of conflict, hence ignores the game theoretic aspects of the problem. Harter (2005) models the situation as a cooperative game and proposes a contract that splits the costs of toilet seat operations evenly among the parties. Both papers agree that the social norm of leaving the toilet seat down in inefficient in the sense that it does not minimize the total cost of toilet seat operations per household. However, both papers fail to address an important concern: If a female finds the toilet seat in a wrong position then she will most probably yell at the male involved. This yelling inflicts a cost on the male. Based on this omission, women may argue that the analysis in these papers is suspect.
In this paper, we internalize the cost of yelling and model the conflict as a non-cooperative game between two species, males and females.We find that the social norm of leaving the toilet seat down is inefficient. However, to our dismay, we also find that the social norm of always leaving the toilet seat down after use is not only a Nash equilibrium in pure strategies but is also trembling-hand perfect. So, we can complain all we like, but this norm is not likely to go away.
All hope is not lost though. An important issue regarding social norms is whether they are created to increase welfare. Are they society’s response to market failures? One such norm is tipping for service quality. Azar (2003) has shown that the norm of tipping increases social welfare. In this paper, we show conclusively that the social norm of leaving the toilet seat down after use decreases welfare and by doing that we hope to convince the reader that social norms are not always welfare enhancing. Hence, there is a case for scientifically examining social norms and educating the masses about the fallacy of following social norms blindly.
The Structure of the Game
The basic ingredients of the game are the same as in Harter (2005). Where we differ from Harter (2005) is the explicit modeling of the costs of yelling.
Consequently, as will become clear shortly, our game is a non-cooperative game of conflict, whereas Harter (2005) models it as a cooperative game. There are two people, one is a representative of the male species, call him John and the other is a representative of the female species, call her Marsha. Initially, they live alone and separately. Each has access to a separate restroom with one toilet. They use this toilet for two operations; #1 and #2. Marsha performs both with the seat in the down position whereas John performs #1 with the seat in the up position and #2 with the seat in the down position. That means, he must change the seat position appropriately before performing the corresponding operation [1]. Assume that the inconvenience cost of changing the seat position is C. Further assume that the need for #1 arises with a probability p. Let’s look at the average costs to John and Marsha:
The average cost to John as a bachelor
Doing #1 this time when he did #2 last time + Doing #2 this time when he did #1 last time:
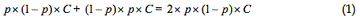
The average cost to Marsha as a bachelorette
Obviously 0 since she performs everything with the seat in the down position.
Now, consider the situation in which John and Marsha decide to cohabit and both use the same toilet. This situation is popularly known as marriage [2]. That changes things for the worse for both parties as far as the toilet operations are concerned. John argues ‘Why does it matter if the seat is up or down? Let’s leave the seat in the position used.” Let’s call that strategy J. Marsha fights back, “It must be down or else.” Or she says, “If you love me then you would leave the seat down.” Let’s call this strategy M. Assume that both John and Marsha use the toilet with the same frequency.
The average cost to husband John from strategy J
Doing #1 and the last user was Marsha + Doing #1, the last user was John and he did #2 + Doing #2, the last user was John and he did #1:
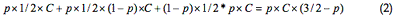
The average cost to wife Marsha from strategy J
The last user was John and he did #1:

The marginal costs under strategy J
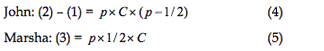
The average cost to husband John from strategy M
Doing #1:

The average cost to wife Marsha from strategy M
Obviously 0.
The marginal costs under strategy M
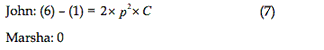
We differ from Harter (2005) in the following:
From this point, Harter (2005) considers the situation as a cooperative game. We differ and consider the situation as a 2-player non-cooperative game with 2 strategies for each player. Suppose Marsha (following M) goes to the toilet and finds the seat in the up position, consequently she yells at John inflicting a cost of D on him. Assume that D >>C . Table 1 shows the payoff matrix.

As can be seen from table 1, there are two Nash equilibria in pure strategies: (J,J) and (M,M).
Proposition 1: The equilibrium (J,J) is not trembling-hand perfect whereas the equilibrium (M,M) is trembling-hand perfect.
Proof: Let e be a very small probability that Marsha trembles to M. Since D >>C, it follows that the Nash equilibrium (J,J) does not survive the trembling hand. By a similar argument, the opposite conclusion is reached for the Nash equilibrium (M,M).
Proposition 2: The equilibrium (M,M) is inefficient compared to the equilibrium (J,J)
Proof: The total cost of strategy combination (J,J) is p2 x C. The total cost of strategy combination (M,M) is higher: 2 x p2 x C.
Discussion and conclusions
For “mankind”, the analysis in this paper has the following appeal: Once again, it has been found that the social norm of leaving the toilet seat down is inefficient; hence, “mankind” may feel vindicated.
For “womankind”, the analysis in this paper is appealing for the following reason: It has been shown that the social norm of leaving the seat down is a trembling-hand perfect equilibrium. Hence, this norm is not likely to go away, at least in the near future.
References
Azar, Ofer H. (2005), “Who Do We Tip and Why? An Empirical Investigation,” Applied Economics, 37(16), 1871-1879
Choi, P. (2002), “Up or down? A male economist’s manifesto on the toilet seat etiquette.” Michigan State Working Paper
Harter, R., (2005), “A game theoretic approach to the toilet seat problem.” Science Creative Quarterly