A PEACH OF A PATHOGEN: CRYPTOCOCCUS NEOFORMANS
(August 2003)
When opportunity strikes you may just find Cryptococcus neoformans making the most of it. Cryptococcus neoformans is pathogen. Cryptococcus neoformans is also an opportunist. Over the past 10 years, infections of this pathogen have been on the rise, mostly striking individuals with compromised immune systems [1]. As an emergent disease it has taken advantage of the recent rise in the rates of immune-suppressing diseases, such as AIDS, as well as the use of drugs that suppress the immune system [1]. This interesting organism is increasingly being placed under a microscope to uncover how it is taking advantage of our immune systems.
A Shake of the Peach Tree
In 1894, a little bit of fermented peach juice introduced the world to an encapsulated yeast-like fungus that we now call C. neoformans [2] (see Figure 1). It was isolated from fruit juice by the Italian Sanfelice and shortly thereafter from the lesions of a woman [3], immediately revealing its potential as a human pathogen. Over the years, the organism Sanfelice first isolated has been re-isolated and given all sorts of names, from Saccharomyces hominis, Cryptococcus hominis and Torula histolytica, all the way to Debaryamyces hominis. This created a little bit of confusion and the name was C. neoformans was finally decided upon to describe all the isolates [4].
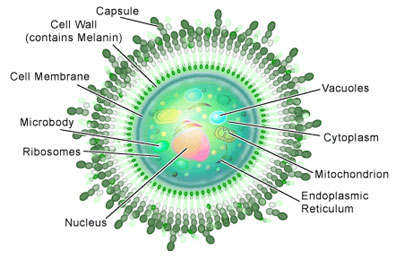
The Basic Biology of C. neoformans
If you examined Cryptococcus neoformans under a microscope you would see round or oval shaped yeast cells, which are often referred to as ‘basidiomycete’ yeast. Some would have a scar on their surfaces where a daughter cell had budded off during reproduction. And if you happened to have some India ink lying around (a dye often used to stain cells) and applied it to them, you would observe a distinctive feature: a capsule made of polysaccharides (see Figure 1).
Basidiomycete fungi of this sort can produce spores, which occurs in another distinctive feature: a club-shaped structure called a ‘basidium.’ The production of spores is a result of the sexual reproduction of C. neoformans (see Figure 2), a process entirely different from its asexual reproduction by budding mentioned above.
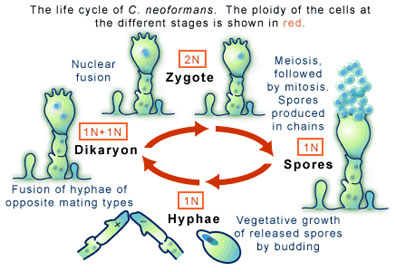
Sexual reproduction in C. neoformans begins when two cells, each carrying one complement of their genetic information (a state in which they are called haploid), encounter one another and, as a result, fuse. The potential to fuse is regulated partly by the two cells being different mating types of which there are two flavors, “a” and “α”. The cycle of sexual reproduction, and thus of cell fusion, involves a series of mitotic cell divisions that produce thread-like extensions called hyphae (see Figure 2). At the end of the hypha the unique structure mentioned above, the basidium, is formed. It is the basidium that will bear the spores (sometimes called basidospores) that will eventually form. For this to occur the two haploid nuclei residing in the basidium must fuse, through an event called karyogamy, to form one diploid nucleus. Meiosis and mitotic divisions will then go on to form spores. As these haploid spores are released to produce more cells the life cycle of C. neoformans will continue.
The Four Varieties
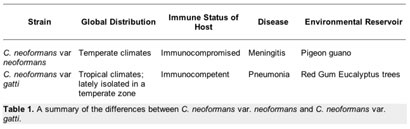
Four different types of C. neoformans occur throughout the world. Each type differs slightly in its global distribution and pattern of virulence. They are traditionally divided based on serotyping into variations A to D [5,6]. Two of the four types (B & C) are called C. neoformans var. gattii, while the others are known as C. neoformans var. grubii (A) and C. neoformans var. neoformans (D). It is the variations grubii and neoformans that are most commonly associated with disease.
In the northern hemisphere the most common forms of C. neoformans are var. grubbi and var. neoformans, which are both most commonly found in pigeon poop [1]. Of the two varieties, it is C. neoformans var. grubbi that makes up the vast majority of clinical strains isolated from infected individuals, while var. neoformans is not normally pathogenic. People who suffer from AIDS or who are receiving immunosuppressive drugs after an organ transplant are at risk of contracting cryptococcosis, the disease for which a C. neoformans infection is the cause [1].
In Australia and other sub-tropical areas of the southern hemisphere the most common form of C. neoformans is var. gatti, making it ecologically and epidemiologically different from C. neoformans var. neoformans and var. grubbi. It is commonly found in association with eucalyptus trees and infections of var. gatti are restricted to lung infections. Interestingly, these infections occur in the immunocompetent population, with an rate of infection is eight per million per year in Australia. Table 1 summarizes the differences between C. neoformans var. neoformans and C. neoformans var. gatti.
Pathogenic Qualities
Cryptococcus as a genus contains approximately 37 species and out of all of them only C. neoformans is pathogenic [4]. This has made it not only a biological curiosity, but also a medical curiosity—especially since there has been a jump in the global rate of C. neoformans infections in the 1980s [1].
It is the occasional inhalation of the basidiospores that cause exposure to the pathogen, although these spores are normally dealt with by the immune system. But, when your immune system is not functioning properly those inhaled cryptococcal cells can reproduce and spread throughout your body. In such a case, cryptococcosis will result; commonly causing meningitits, which is an inflammation of the membranes surrounding the central nervous system (the brain and spinal cord). The incidence of cryptococcal meningitis being about ten per million per year, usually located in urban centers. Cryptococcosis has also been found to cause pneumonia and skin lesions.
The rise in C. neoformans infection is commonly linked to a global increase in the numbers of immunocompromised individuals, mostly closely associated with the AIDS epidemic [7]. The incidence of HIV-infected patients that develop cryptococcosis is around 10-15% in the Western Countries, but the effect of C. neoformans on AIDS is crystallized in Zimbabwe were the number jumps to 88% [8].
A Changing Picture of where C. neoformans is found
A traditional picture of the distribution of C. neoformans (see Table 1) and the incidence of cryptococcosis is beginning to change. Case in point, an outbreak of C. neoformans var. gatti infections on British Columbia’s Vancouver Island [9]. A surprise to everyone, since this is the type of Cryptococcus is normally restricted to Australia. In 2001, British Columbia also saw an increase in the cases of cryptococcosis in pets, accompanied by a concomitant increase in the number of human cases.
The British Columbia Centre for Disease Control (BCCDC) launched an investigation into the disease. The detailed analysis that followed took a close look at medical records, undertook clinical reviews of all confirmed cases, environmental sampling, the identification of the pathogenic strains by genetic fingerprint analysis, and geographical mapping of the incidence of the disease.
As the results came in, it was found that since 1999 there have been over 40 incidences of cryptococcosis on Vancouver Island—all caused by C. neoformans var. gatti. The incidence of C. neoformans var. gatti, both in clinical and environmental samples, was found to be the highest on the central east coast of Vancouver Island. Visiting Rathtrevor Beach, a popular park in the area, turned out to be a significant risk factor for acquiring cryptococcosis. This was of interest since C. neoformans var. gatti is commonly found in association with Douglas fir, Garry Oak, Arbutus and Cedar trees. Activities like branch clean-up and chopping wood were thus found to be protective against cryptococcal illness. In 2001 the infection rate has peaked at 20 cases per million per year.
The BCCDC analysis has answered many questions about the outbreak of cryptococcal illness on Vancouver Island, but others remain. How did C. neoformans var. gatti ended up on Vancouver Island? The fungus could have “hitch-hiked” here via infected trees imported from Australia or just naturally expanded its ecological niche due to climate changes. And more importantly, what has changed to increase the virulence of this fungus in comparison to its Australia counterpart?
Researching the Virulence of C. neoformans
Researchers have been working to determine how C. neoformans causes disease in humans and the bulk of this effort has been directed at understanding its virulence factors. Several have been identified and two of the most heavily studies are the secretion of a polysaccharide capsule and melanin synthesis [1].
Polysaccharide capsule—In response to low levels of iron in its environment and physiological levels of CO2, C. neoformans can synthesizes a thick polysaccharide capsule. The capsule interferes with the action of special immune system cells called macrophages that devour invading cells, thus protecting the C. neoformans cells from the immune system. Additionally, if macrophages do manage to engulf the cryptococci the capsule allows it survive and reproduce inside of the macrophage.
Melanin—This dark pigment is produced by the polymerization of compounds called polyphenols. It is a compound similar to the one that makes moles and freckles dark brown. For Cryptococcus, melanin offers protection from a process called oxidative killing. In host immune cells like macrophages, the killing of foreign cells is accomplished by exposing the engulfed foreign cells to highly reactive molecules called free radicals, which will react with molecules like DNA and proteins. These uncontrolled reactions often prove fatal. Melanin serves to protect cryptococci cells by reacting with free radicals to neutralize them.
Each of these factors aids in the survival of C. neoformans within its host, allowing it to evade the immune system and thus cause disease. It is for this reason that they are labeled as virulence factors.
Filling in the Gaps
It was over a hundred years ago that C. neoformans was discovered and since that time it has been scrutinized as a pathogen. But with cryptococcosis emerging in the past twenty years as one of the most-life threatening diseases in immune-compromised individuals, our understanding of its biology and pathogenic qualities is in need of gap filling. The medical research machine has been accelerating its focus on C. neoformans and many new discoveries are springing free, certainly making it a topic to keep your eye on.
Additional Reading
1. Casadevall A, Perfect JR. (1998). Cryptococcus neoformans. Washington DC: ASM Press. 541p.
2. Segal E, Baum GL. (1994). Pathogenic Yeasts and Yeast Infections. Boca Raton: CRC Press. 238p.
3. Howard D. (2003). Pathogenic Fungi in Humans and Animals. New York: Marcel Dekker
References
1. Buchanan KL, Murphy JW. 1998. What Makes Cryptococcus neoformans a Pathogen? Emerging Infectious Diseases 4(1): 71-83.
2. Sanfelice F. 1895. Sull’azione patogena dei bastomiceti. Ann Inst Igien Univ Roma 5: 239-262.
3. Knoke M, Schwesinger G. 1994. One Hundred Years Ago: The History of Cryptococcosis in Greifswald. Medical Mycology in the Nineteenth Century. Mycoses 37: 229-233.
4. Mitchell TG, Perfect JR. 1995. Cryptococcosis in the era of AIDS—100 years after the discovery of Cryptococcus neoformans. Clin Microbiol Rev 8:515-548.
5. Levitz SM. 1991. The ecology of Cryptococcus neoformans and the epidemiology of cryptococcosis. Rev Infect Dis 13: 1163-9.
6. Franzot SP, et al. 1999. Cryptococcus neoformans var. grubii: Separate varietal status for Cryptococcus neoformans serotype A isolates. J Clin Microbiol 37: 838-840.
7. Powderly WG. 1993. Cryptococcal meningitis and AIDS. Clin Infect Dis 17: 837-842.
8. Hakim JG, et al. 2000. Impact of HIV infection on meningitis in Harare, Zimbabwe: a prospective study of 406 predominantly adult patients. AIDS 14: 1401-1407.
(Art by Jane Wang – note that high res versions of these image files are available here)