PREDICTABILITY IN THE GAME OF WAR
Appraise war in terms of the fundamental factors. —Sun Tzu
The card game of war is typically considered a children’s game, as it requires no skill to play and minimal understanding of playing card relationships in a standard deck. With skill eliminated as a factor in determining the outcome, it is often assumed that war is simply a random game of chance. Yet the game cannot be purely determined by chance, as the initial conditions of the game must have some bearing on the final state. The existence of random factors in the game do not allow for the claim that war is a deterministic game, yet it is still possible to quantify properties of the initial state that are indicative of a victory probability.
The Rules of War
The traditional game of war uses a standard 52-card deck of playing cards divided evenly and randomly between two players. Neither player is allowed to view their hand or rearrange it. The players simultaneously reveal the top card of their deck on the table, and the player with the higher value takes all cards on the table. Cards won from a particular trick are gathered and added to the bottom of the victor’s deck. Suits are disregarded in war, making it an ideal game for exposing young players to concepts of inequality. If both players reveal cards of equal value, a war commences: each player plays two face-down cards on the table and reveals a third card that decides the victor. It is possible to play two, three, or more iterations of a war before the revealed cards are not equal, but in most cases one iteration will suffice to decide the outcome. The victor gains all cards played in the war, including those played face-down. This is the only way in which a player may capture an opponent’s aces. A player loses the game when all of their cards have been captured or exhausted.
Variations in the game of war include varying the number of face-down cards in a war to one, three, a random value, or a plethora of other dependencies. The other major variation consists of placing all cards won from tricks in a separate pile until the player’s deck is extinguished. These cards are then shuffled and used to continue the game. None of these variations is significant enough to differ from the standard rules above when considering a long term analysis. Other variations of war exist in plenty, but most of these have additional rules that warrant their classification as a different game.
Collecting Game Statistics
A computer simulation of war provides a robust and rapid method for examining deterministic tendencies of the game. This simulation used the Mersenne twister random number generator, which has a period much greater than is required for an analysis of this magnitude. Ten million games of war generated a set of three characteristics. The first, and most obvious, statistic is victory. One might guess that in lieu of any deterministic factors, the outcome of a game of war would be no different than tossing a coin. Two other values were also calculated based on a player’s starting hand: deck weight and initial advantage.
Deck weight is a measure of the relative strength of a player’s starting 26 cards. Given that there are 13 different numerical card values (two through ace), define the weight of the card with the numerical value “8” to be 0. Defined as such, the cards [9, 10, J, Q, K, A] would have weights of [1, 2, 3, 4, 5, 6] respectively, and likewise the cards [2, 3, 4, 5, 6, 7] would have respective weights of [-6, -5, -4, -3, -2, -1]. The deck weight is then defined as the sum of the weights of a player’s initial 26 cards. The weight of an entire 52 card deck is 0, as would be the case for each player in a perfectly divided game of war (for example, one player is dealt all the reds while the other all the blacks). In a game not so evenly divided, the weight of one player’s deck is equal to the opposite of the other player’s deck (since the weight of the entire 52 cards must vanish). The maximum possible deck weight for a player is 84, which would ensure certain victory. In general, a large deck weight may be indicative of a player’s advantage over their opponent, at least concerning card values.
While the deck weight may suggest a certain type of advantage, the ordering of the cards in war is equally important. The initial advantage is defined for a player as the number of tricks won minus the number of tricks lost, over the first iteration through their deck. If no wars occur in the first 26 cards of play, it would be expected on average for a player to have an initial advantage of 0. The maximum initial advantage of 26 would give a player sure and swift victory. For any particular game, a player with a large initial advantage will be in possession of a majority of the cards once all initial 26 have been played. After this point, though, the random element of placing cards won at the bottom of a player’s deck renders the initial advantage measurement useless any further prediction. At best, it is an indicator of the depedence of final victory on the initial ordering of the cards.
Simulation Results
The average cases for both statistics are as expected: the mean deck weight and mean initial advantage are both 0, with both statistics normally distributed about a mean of zero at a 99% confidence level. Deck weight is distributed with a standard deviation of 13.62 and initial advantage with a standard deviation of 4.69. It is interesting to note that even with 10 million games, the maximum and minimum values of the weight and initial advantage did not occur once. Of course, these states are also highly improbable. Neither histogram corresponds exactly to the normal distribution, but the agreement is well within acceptable statistical significance.
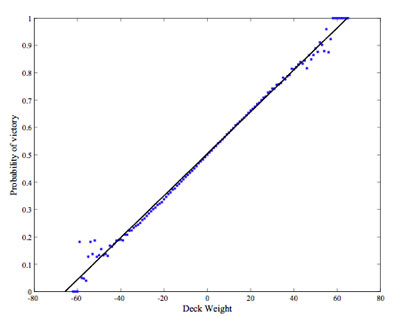
Figures 1 and 2 are plots of the probability of victory versus deck weight and initial advantage, respectively. The relationship between deck weight and victory shown in figure 1 is clearly linear, at least for a deck weight between -40 and 40 (or 3σ). At magnitudes greater than 40, the number of sample games decreases sharply allowing the bounds on the victory probability to be less constrained. Fitting a line to this data with linear least-squares yields the equation
where W is the deck weight and p(W) is the probability of victory. This line fits the data with a correlation of R2=0.994. With a deck weight W=0, the probability of victory is nearly 50% as expected. Although on average a player will win and lose an equal number of games, predictability is possible once the deck weight is determined. The probability of victory improves to 60%, 70%, and 80% respectively for deck weights one, two, and three, standard deviations from the mean.
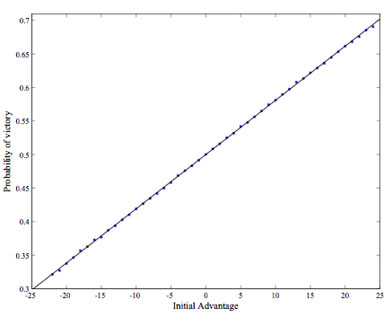
The relationship between initial advantage and victory is illustrated in figure 2. This trend is even more markedly linear than figure 1, with no points significantly deviant from a linear regression. This can be attributed to the smaller range of values (-26 to 26) of initial advantage compared with deck weight. The fit linear relationship between these two variables is
where A is the initial advantage and p(A) is the probability of victory. This line fits the data with R2=0.999, even better than the relationship in figure 1. For this statistic, the victory probabilities at one, two, and three standard deviations from the mean are 54%, 58%, and 61%. Though the relationship is apparent between A and p(A), the degree to which initial advantage is useful in prediction is low. An initial advantage of 26 would win the game automatically, but a slightly lesser value of 24 does not even win 70% of the time. Prediction based on initial advantage seems to be of higher risk and lesser certainty.
Deck weight is a useful indicator of victory probability, and is easily obtained by keeping a cumulative total of the weight as the first 26 cards are played. However, the question of applicability now comes into focus: the weight of the deck is only known after play has begun. Perhaps the cunning player could casually make a friendly wager once they discover their own advantage. Or, those slight of hand could stack the deck in their favor enough to tip the balance—but not enough that suspicions are aroused. But of course, fair game play is always the best course of action. Perhaps the ability to impress an opponent by making an early prediction will suffice, as we sing with Edwin Starr: War. Huh. Yeah. What is it good for? Absolutely nothing!