THE MURPHY’S LAW EQUATION
There are many laws in the physical sciences, most of which have mathematical equations that govern them. Widely know laws such as the laws of electricity and magnetism, have Maxwell’s equations. Fluid-flow is governed by the Navier-Stokes equations, and of course everyone is familiar with Einstein’s energy to mass relation, E=mc2. Why then does an equally relevant and useful law, Murphy’s Law, have no such foundational equation? In what follows I present an equation to predict the outcome of Murphy’s Law.
The law, in its simplest form, states:
“If anything can possibly go wrong, it will, and at the worst possible time”
After beginning work on this project, previous work was uncovered. The work is minimal, but there has been at least one other notable attempt1 at generating an equation for Murphy’s Law. This equation however does not fit recorded data very well, and is very complex. More careful analysis of the Law and recorded data, as well as personal experience, have led me to the following new equation (the derivation of which I have not included here), called Murphy’s Equation:
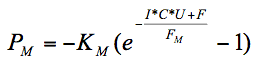
Here, PM is the Murphy’s probability that something will go wrong. KM is Murphy’s constant (equal to one) and FM is Murphy’s factor, a very small number that can only be calculated on a 386-computer running Windows 3.1. Here we will approximate it by FM ≈ 0.01. Similar to previous work, I, C, U and F are parameters on a scale of 1-10 describing the situation of interest. I is the importance of the result or outcome of the event, C is the complexity of the system, U is the urgency and F is the frequency. From these 4 parameters, virtually any event can be described. Plugging those numbers into the equation with the appropriate constants will then give the probability of at least one thing going wrong. To get an idea of how this works, lets look at some specific cases.
First, to start with a simple example, lets calculate the probability of the clutch on a 1989 Toyota Tercel ceasing to function 100km from home at night in the middle of a rainstorm. The importance of the clutch working in this situation is obviously high, but no one is dying, so lets estimate an 8. The system is fairly simple compared to other systems in the car, so C=5. It would be nice if the clutch worked soon, so the urgency U would also be around 8. Finally, the clutch only needs to work for one drive home, so the frequency is low, say F=1. Now, putting these parameters in Murphy’s Equation shows that PM=1. Comparing to experimental data, this number matches exactly, as the clutch did indeed cease to function at this time. Repeating this calculation with I=7 also gives PM=1, showing the robustness of this equation.
Moving to a more complicated example, lets examine the case where the clutch has failed in the above example, but calculate the probability that the flashlight needed to inspect the clutch doesn’t work, the front half of the hazard lights on the car don’t work and that the trunk where the few tools are kept has 3” of water in it (remember its raining). In this case, Importance is about the same, an 8 or so (its hard to justify higher than this without a life or death situation). Here, C=4, as the flashlight, hazard lights and trunk are all fairly simple systems. Because it is raining and the driver is now stranded, the urgency can be bumped up to a 9, while F=3 (three events need to occur). Putting these values into the equation gives a PM of 1, which is indeed what did happen, showing that again this equation matches experimental data very well.
In summary, the equation presented here gives a new mathematical foundation to one of today’s most recognized physical laws, Murphy’s Law. Experimental data matches very nicely with the theory presented in this equation, and the author expects further testing will yield equally positive results, and hopefully the adoption of this equation as a metric for predicting how often things really do go wrong for no good reason.
References:
1) “The formula that proves that ‘Sod’s Law’ [Murphy’s Law] really does strike at the worst possible time” British Gas News, October 7, 2004.